CONWAY’S GAME OF LIFE MODEL

The canonical Cell Matrix model

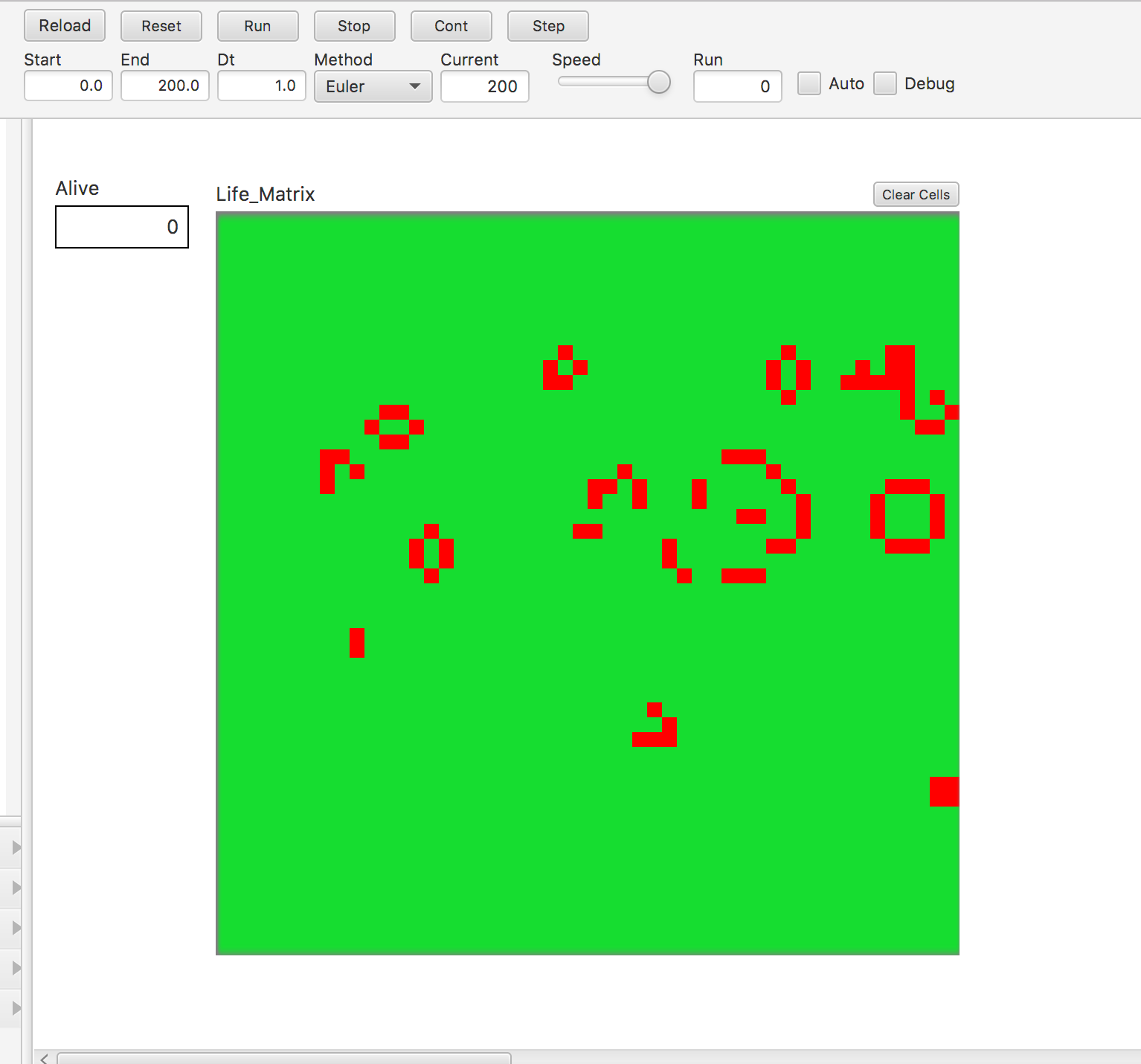
Conway’s Game of Life is often the first agent-based model that is discussed in computer science classes. This is because the programming is relatively simple,

using just a few basic rules to define the entire model. Each tile is defined to be either alive or dead. This is done in the cell submodel with the use of a simple 1 for

alive, and 0 for dead. The rules of the game of life are as follow:

• If you have 1 or less living neighbors, you die or remain dead (loneliness).

• If you have 2 living neighbors, you remain dead or remain alive (persist).

• If you have 3 living neighbors, either come to life if you are dead, or stay alive if you are already alive.

• If you have 4 or more living neighbors, you die or remain dead (overcrowding).

Each tile has a total of 8 neighbors (except for the boundary tiles). The initial condition is automated to be an interesting configuration in which a lot of richness

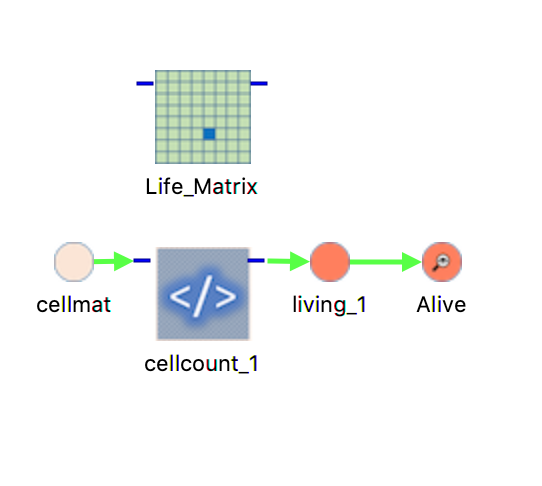
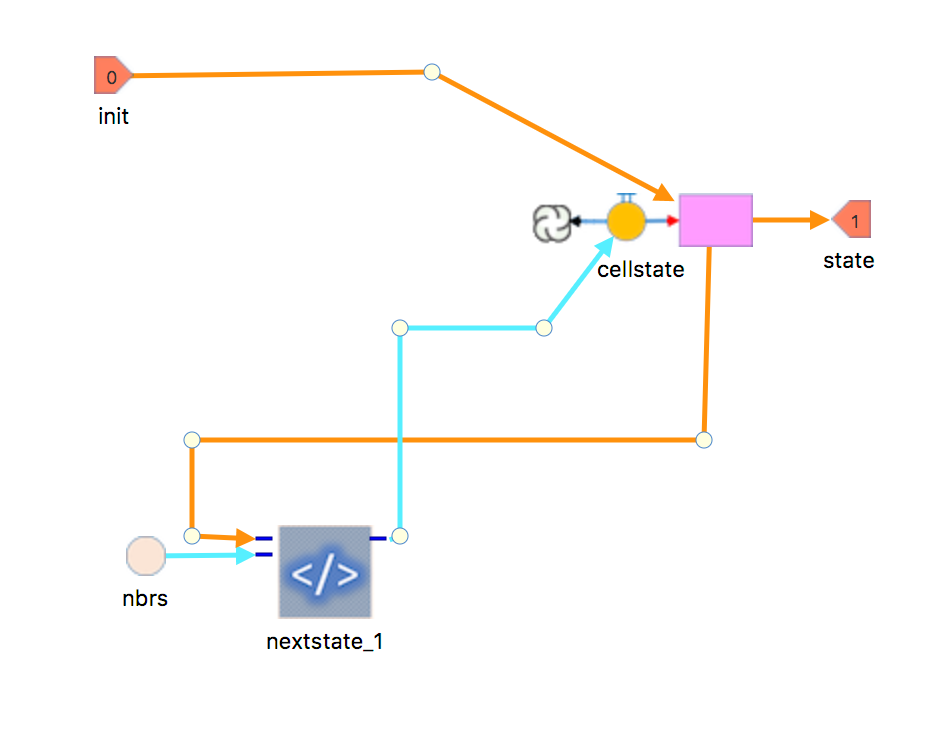
comes out over a long period of time. The way the cells actually work, is by having a cell count the number of “alive” neighbors around it (Neighbors are computed

at the beginning of the simulation in a code chip and stored in a property); the result of the computation send either a 1 or a 0 throw a flow and into a stock which is

set to be a discrete value, meaning its value is reset every turn.

You also have the ability to click on tiles before the run, and change their state in order to change your initial conditions.

LIFE CAPSULE

CELL CAPSULE

MODEL LAUNCH