TWO-WELL CHAOS MODEL

The model shows the results of the Duffing equation, displaying chaos in movement. This model builds directly on the damped spring model, but this time we’re using a

nonlinear spring. This can be represented as a cart with two hollows in it that are separated by a hill. If the cart is shaken by an oscillating force, then a marble placed in one of

the holes will oscillate in the hole, and then, unpredictably, will move over the hill into the other hole. The unpredictability of the marble’s movement makes this a chaotic

model.

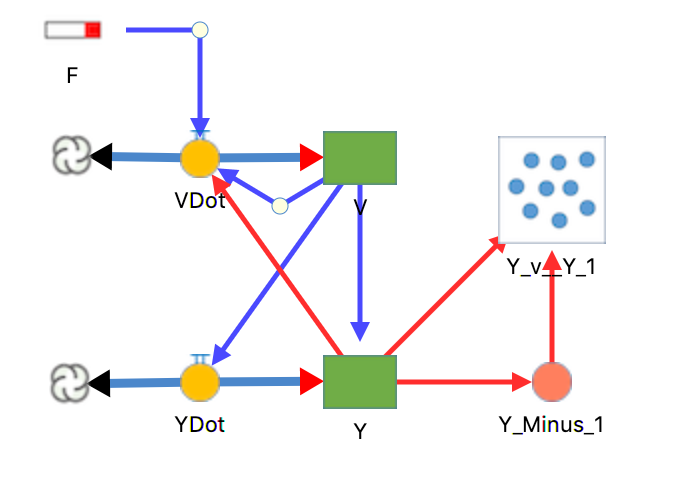
The model contains two stocks, V, and Y which are initialized to 0.0. V has a flow VDOT with

VDOT= -V/3 + Y – Math.Pow(Y, 3) + F*COS(TIME()),

where F = 0.1. Y has a flow labeled YDOT with

YDOT=V. 

Graphing Y(t) against Y(t-1) in a scatter plot, we can see that every time the sign of Y changes, the ball moves to the other hollow. If there is no sign change, the ball has moved within a hollow.

**From Dynamic Modeling by Bruce Hannon & Matthias Ruth, Ch. 37.4.

MODEL:

MODEL LAUNCH:

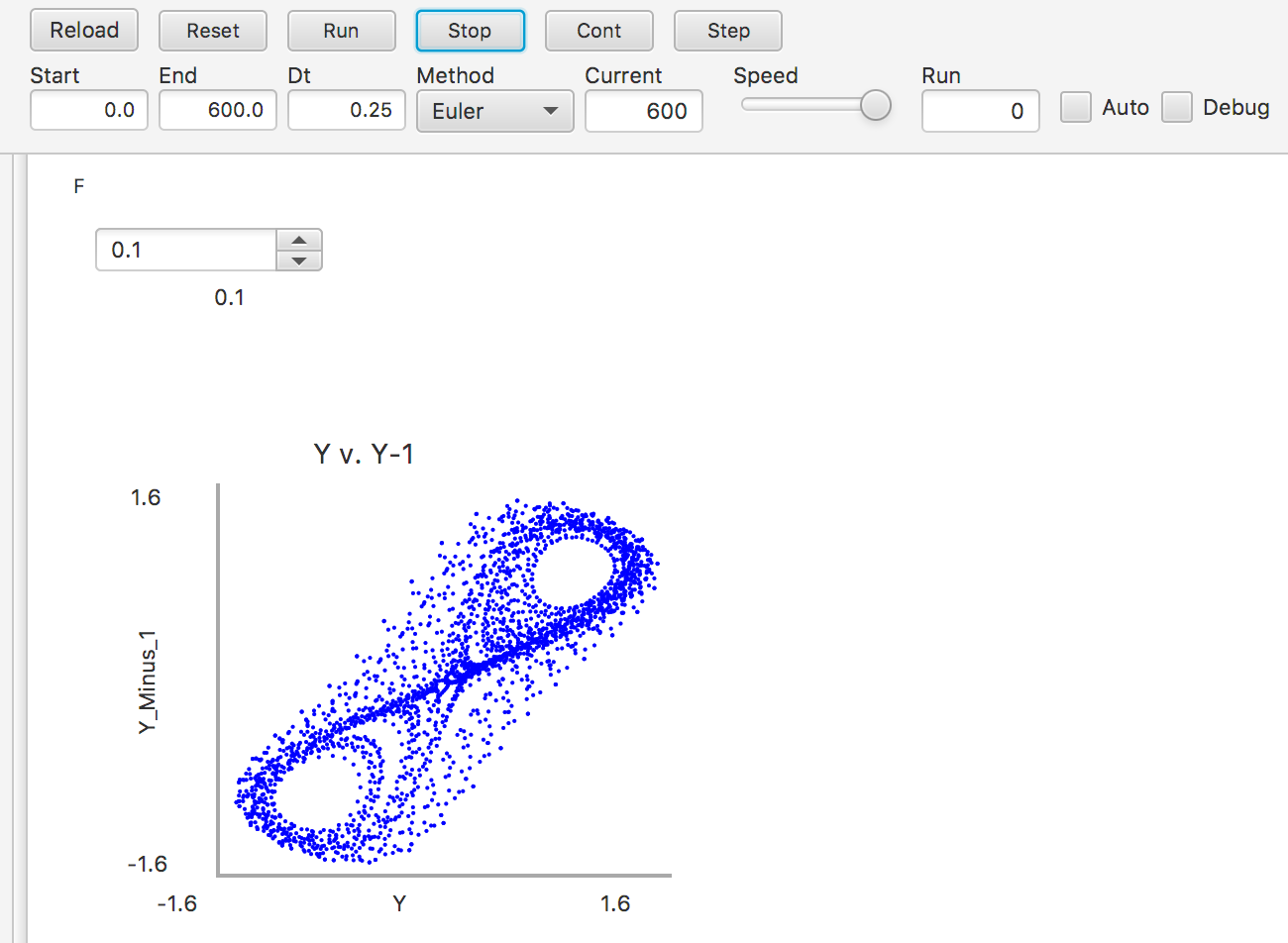
Take notice here of the End time, of 600.00.  Now observe what happens with an increased End time, such as 2000.00:  

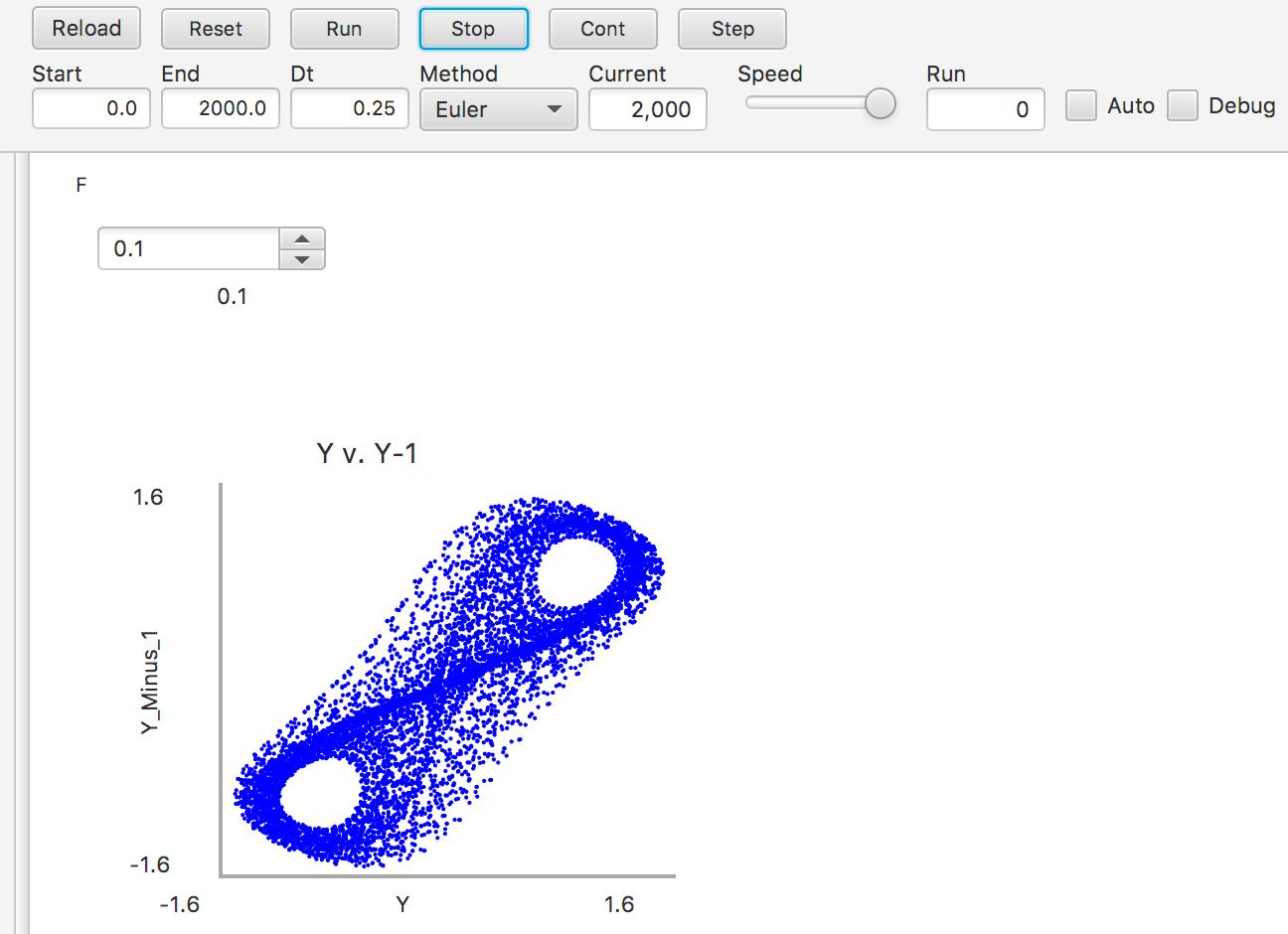
 The model demonstrates a difference in densities, as expected by the results of the Duffing Equation.  Similarly, take liberty to experiment with the other Sliders and

values available in this model.